データを読もう
過去の当選番号のデータは、CSVファイルで下記のようにdata.csvに保存しています。
現在は第1386回くらいになります。
第1回,2,8,10,13,27,30 第2回,1,9,16,20,21,43 第3回,1,5,15,31,36,38 第4回,16,18,26,27,34,40 第5回,9,15,21,23,27,28
過去のデータを基に当たり番号を予想するので、まず過去のデータを読む必要があります。
読み込みは、前回作成した関数の中で行い、データ変数はグローバル変数としました。
csvファイルの読み込みは
with open(‘data.csv’,’r’) as f: として行います。もうおまじないだと思って進めましょう
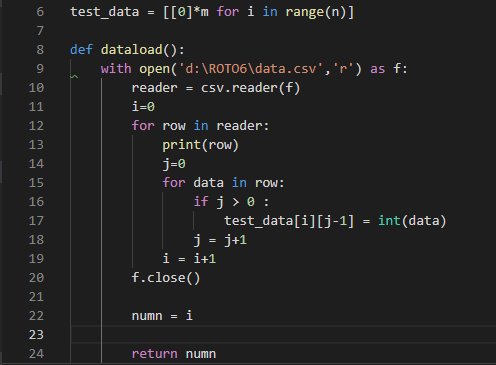
test_data = [[0]*m for i in range(n)]
def dataload():
with open('d:\ROTO_6\data.csv','r') as f:
reader = csv.reader(f)
i=0
for row in reader:
#print(row)
j=0
for data in row:
if j > 0 :
test_data[i][j-1] = int(data)
j = j+1
i = i+1
f.close()
numn = i
return numn
まず1行ずつ読んで、その1行からそれぞれ1個ずつのデータを取り出し、文字列を整数に変換して保存しています。
最初に’第1386回’という回数を保存しているので、それは読み飛ばします。
確認しよう
Pythonの配列は少し奇妙でもあったのでちゃんと保存されているか確認しましょう。これは、確認できて、次へ進める時は削除しても良いでしょう。
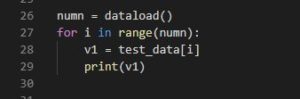
numn = dataload() でデータ読み込みの関数を呼び出し、データ自体はグローバル変数に保存して、データ個数を戻り値として返しているので、numnにデータ数を保存します。
numn = dataload()
for i in range(numn):
v1 = test_data[i]
print(v1)
そして、データ数だけリスト型のデータを表示します。
結果は
[2, 8, 10, 13, 27, 30] [1, 9, 16, 20, 21, 43] [1, 5, 15, 31, 36, 38] [16, 18, 26, 27, 34, 40] [9, 15, 21, 23, 27, 28] [6, 12, 23, 25, 28, 38] [7, 19, 21, 23, 33, 35] [11, 16, 18, 20, 42, 43] [11, 19, 23, 38, 39, 42] [1, 3, 19, 21, 35, 39]
の様に、正常に表示されました。
これはしばらくこのままで様子を見ましょう。
あたり番号を予測する・・・ 何回出現したか
過去のデータは揃いました。データ箱に入りました。
今度はそれを基にあたり番号を予測します。
といって、数学的にそのような数式はあるのでしょうか。
あれば、ロト6は閉鎖されているでしょうね。
ここからは、私の勝手な推論であたり番号を予想してみます。
もっと、ちゃんとした考え方があるという方は、。ご連絡をお願いします。
1.1~43の数字は最終的に均等に出現する。
これは、紛れもない大原則でしょう。
これが成立しないということになればロト6の信用はないでしょう。
ということで1~43の数字の出現回数を調べてみましょう。
これも、関数にして、関数を呼ぶ形で計算する。
その前に、その結果を入れる箱を用意しておく、1つの数字あたりに出てくる変数は1つではないだろうから、とりあえず3つ用意しておく。
result[N][0]に出現回数を保存する。
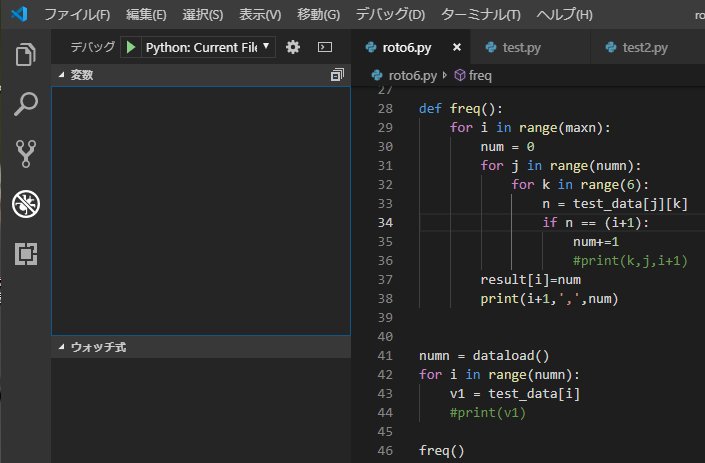
出現回数を数える関数
その結果をファイルに保存し、エクセルで整理してみると。
result = [[0]*3 for i in range(maxn)]
def freq():
for i in range(maxn):
num = 0
for j in range(numn):
for k in range(6):
n = test_data[j][k]
if n == (i+1):
num+=1
#print(k,j,i+1)
result[i][0]=num
#print(i+1,',',num)
freq()
for i in range(maxn):
print(result[i][0])
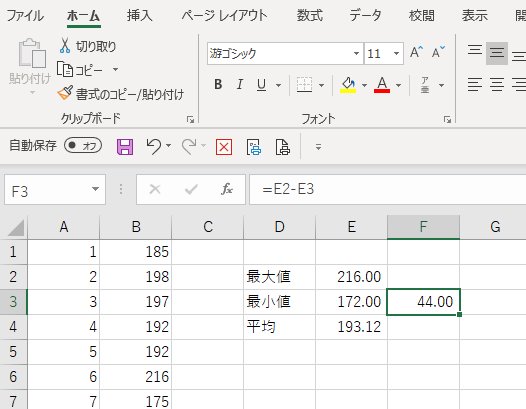
43個の出現回数から最大、最小そして平均を計算
1386回×6=8316回あたり1/43の確率だから、平均的な出現回数は193.4回となる。
最大と最小の差は44回、これを多いとみるか少ないとみるか、判断は難しいが。
すべての数字に均等に機会があるものとすれば、出現回数が少ないものは、これから出てくる確率が高いと言えないだろうか。
まだ、過去データから想定できることはありそうだ。
出現回数に傾向はないか、1枠~6枠には出てくる数字にある幅があるのでは、1枠に43が来ることは何のだから。
それも、過去データを見ればわかるかも。
ということを次回に