シニアだってブログもプログラムもできるよ
なにを今更寝ぼけた話を・・・ということになるが
前回は開発環境を変えて、配列のライブラリの使い方を勉強して、これまでの当選番号には若干バラツキがあるが、ほぼ均等にそれぞれの番号は出現しているらしいことが分かった。
しかし、問題はその出現の仕方である。全くランダムに出てきているなら、せいぜいこれまでの出現回数の多寡くらいしか予測の情報は無いことになる。
これまでの当選番号の出現の仕方について少し整理してみる。
下の図は、各番号のこれまでの累計の回数の変動図である。
Pythonを扱うのにVSCODEを使ってきた。Debugの昨日も付いているし一々コマンドプロントとエディターの間を行き来する必要もないから。
しかし、PythonにはIDLEという開発環境がPythonと一緒にインストールされる。
このIDLEでもデバッグは可能だし、IDLEから実行も可能なので暫くIDLEを使ってみることにした。
過去の当選番号のデータは、CSVファイルで下記のようにdata.csvに保存しています。
現在は第1386回くらいになります。
第1回,2,8,10,13,27,30 第2回,1,9,16,20,21,43 第3回,1,5,15,31,36,38 第4回,16,18,26,27,34,40 第5回,9,15,21,23,27,28
過去のデータを基に当たり番号を予想するので、まず過去のデータを読む必要があります。
読み込みは、前回作成した関数の中で行い、データ変数はグローバル変数としました。
どんなプログラムにせよ、一連の作業をひとまとめにして関数とする。
Pythonも同様だが、その姿は全く同様ではない。
普通は関数は
void func1(int nn)
{
・・・・・
return(f);
}
等のように始まり'{‘と終わり’}’がある。
しかし、Pythonの関数はif文やwhile文あるいはfor文も同様で
for i in data: 処理１ 処理２
ここで終わり、はじめは何となくわかるが、終わりがわからない。
ドアを開けて閉めずに行ってしまう、行儀の悪い奴、みたいな感じ。
前回のtest.pyではリスト型に直接データを書き入れた。
しかし、これでは1400×6個のデータを書き込む必要があるし、追加のたびにソースを開いて修正する必要がある。
当然、データファイルを用意してそれに追加データを書き込み、プログラムはそのファイルから読み込むことになる。
で、その前にtest.pyの初期入力のリストデータを後から追加する形に変更した。
test_data = [[0]*3]*3 v = 1 for i in range(3): for j in range(3): test_data[i][j] = v v += 1 for v in test_data: print(v)
リスト型2次元配列（３×３）を用意して一つずつインクリしてデータに書き込んでいく。
この結果を表示させる。
当然結果は
[1,2,3]
[4,5,6]
[7,8,9]
となるはず・・・
結果を見てみよう
[7, 8, 9] [7, 8, 9] [7, 8, 9]ヌヌヌヌ
こんな筈はない。正直、そう思って、ほぼ一日イングリモングリ考えたりソースを書き換えたり。
宝くじを当てよう、というと語弊があるので少し修正すれば、ROTO6を勉強してプログラミングで当選確率を上げよう、という企画です。
前にも書いたように、プログラムは目標を達成するための道具です。
目標に向かって、必要なことから勉強していくのが私のやり方。
金銭欲、性欲、睡眠の三大欲（違ったかな）の達成のためにプログラムを勉強する。
勉強する意欲がわくでしょう。
少なくとも、サイコロで選ぶのではなく、自分の考えた理屈で番号を選べば外れたにしても納得がいくし、別の考え方を模索する。
ロト６は、１～４３の数字から６個を小さい順に選ぶくじなので、その組み合わせは・・・とてつもない組み合わせになります。
ただ、この６個の数字になにか法則はないだろうか、まずそれから探していきたい。
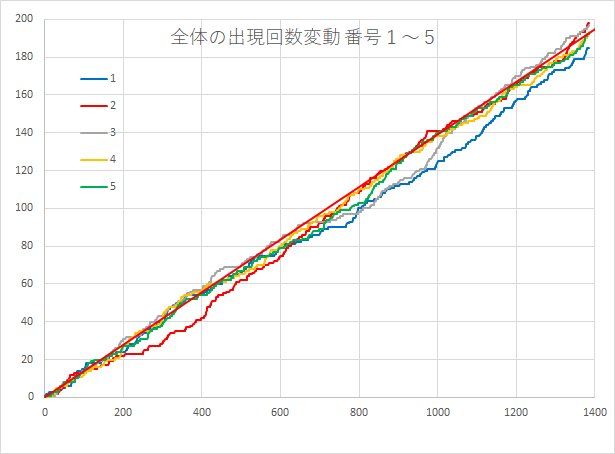
当然、１～４３の数字のなかから一つの数字が選ばれる確率は1/43になる。
今現在抽選回数は1400回弱なので、１つの数字が出現する回数は1400*6/43=195回、過去のデータを調べて回数が少ない数字はこれから出てくる可能性は大きい。
また、調べた結果１～６の当選組み合わせは、この１４００回弱のなかで一度も重複していない。
１桁～６桁それぞれの桁で出現する可能性のある数字はある確率で予想できる。
つまり、1,2,3,4,5,6という組み合わせや38,39,40,41,42,43という組み合わせは非常に確率が低い。
これ以外にも過去のデータから出現する傾向というものが得られるかもしれない。
これは、データ数が多いこともあり、プログラムに持ってこい、ということになる。